Using pedigree information in QTL discovery and genome-wide predictions
- Umesh Rosyara
- Jun 4, 2014
- 4 min read
In this post I will discuss about how pedigree information can be used in identity-by-descedent method based QTL discovery, breeding values and genome-wide predictions using bayesian MCMC based approach.
QTL mapping in biparental population has been popular for its simiplicity and power if conditions are met such as family size, marker density. QTL discoveries are usually based on narrow set of germplasm (mostly germplasm from wide crosses) thus limit discovery of important QTL alleles relevant to fine tune the results. Also little is known for their robustness and background specific role. Including pedigree information in QTL discovery can widen the genetic base and potential alleles or loci discovered as significant otherwide are missed.
For traits of low heritability it is often difficult to discover QTLs, thus genome-wide predictions are popular as they can use whole genome information. The genome-wide predictions usually are based on identity by state concept, but with pedigree information we can include strength of IBD into predictions which is particularly useful for biallelic markers. Genome-wide prediction can be done by :
(1) Only significant regions - QTL mapping and breeding value estimation based on the regions - the genome-wide predictions based on BayesC, also known as Bayesian stochastic search variable selection are in this line of finding signficant regions.
(2) Whole genome - traditional genome-wide prediction used in genomic selection where we use all loci.
In this context, whenever we have, pedigree information can be a great value potentially add power. The following is summary on how we use the pedigree information in QTL discovery and genome-wide predictions using MCMC based baysian analysis.
The model
Using a linear model, the phenotypes y can be described by an intercept μ, environmental effects b, a pedigree-based polygenic effect u, regressions on the QTL covariates a, and a model residual e, as
y=1μ+Xb+Zu+Wa+e ........................................................ (1)
where X is the design matrix for environmental effects, and Z and W are design matrices that link polygenic and QTL effects to
the observed phenotypes.
The Infinitesimal model (TIM) for polygenic effects
The idea of the infinesimal model comes in to increase the predictions or estimations or heritability as usually many loci with small QTL effects are missed (remain undetected) in many mapping experiments.
Genetic models
A bi-allelic model is assigned to a QTL with alleles denoted by Q and q, resulting in three genotypic classes: QQ, Qq/qQ, and qq. For each effect, i.e. additive and/or dominant, of each QTL, one column is included in W. The covariate values of [QQ Qq qq ]are equal to[1 0 −1] and [0 1 0] for additive and dominant effects, respectively.
The frequency of the allele Q among founder individuals is denoted by fa and the linkage map positions of the QTL are given by vector λ. The QTL genotypes of individuals are a priori unknown and modeling is based on independent assignment of alleles to founders and segregation indicators to trace transmission from parents to offspring.
Segregation indicators
Important part of any identity-by-descedent method is derivation of segregation indicators. The following small pedigree provides an example of segregation indicators.

Prior assumptions
Bayesian modeling assigns normal priors to the vectors u, a, and e

where σ^2u is the polygenic variance and A is the numerator relationship matrix based on known pedigree records, σ^2a is the per-QTL explained variance, and σ^2e is the residual variance.
Posterior sampling by MCMC simulation
Markov chain Monte Carlo (MCMC) simulation can be used to obtain samples from the joint posterior distribution of the variables in the probability model (1).
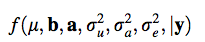
Heritability and Variance expained by single QTL
The heritability can be calculated as:
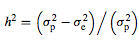
QTL heritability can be expressed as:


QTL genotype assignment
The analysis can be done using different bin size. For each individual the stored samples of QTL genotypes (QQ, Qq, and qq) can be used to estimate posterior probabilities of QTL genotypes for the bins that exceeded the posterior inclusion probability threshold. We can examine certainty on the posterior genotype probabilities, denoted as p(gtp|y), by:
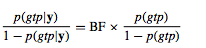
where p(gtp) denoted the prior genotype probability.
Genomic breeding values
The breeding value can calculated at different level - QTL, chromosome or genome.

with w i,q refers to the (i,q) element of design matrix W in Eq. (1). The calculation of the genomic breeding values in the above equation is identical to Bayesian methods for genomic selection (see Meuwissen et al. 2001)
Sum of Breeding values for significant genomic regions
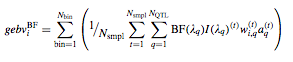
where BF(λq ) is an indicator variable with value 1 if the positional bin λ q has a Bayes factor exceeding a threshold ( usually positive if >2 or strong if greater than >5) evidence and zero otherwise.
Breeding values for each significant regions.
The bin-wise breeding values can be used to track most important genomic regions that are contributing the individuals genomic breeding values.
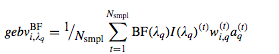
For More Details:
Rosyara U. R. et al.2013. Fruit size QTL identification and the prediction of parental QTL genotypes and breeding values in multiple pedigreed populations of sweet cherry. Molecular Breeding 32: 875-887.
Comments